Joan Taylor's Tilings
Eve to llama tiling
| Home |
| Eve tiling and variants |
| Rhombus seed tilings |
| Square tilings |
| Triangle and 3-fold symmetry tilings |
| Cross & 3 key tiles |
| Eve to llama tiling |
| 2 Squares tiling |
| Cube tiling |
 8 Triangle set 1 PDF 6.7MB |
 8 Triangle set 2 PDF 5.5MB |
 8 Triangle set 3 PDF 6.3MB |
 Chiral pattern PDF 7.8MB |
 2Hex 1 triangle PDF 6.6MB |
 1 Hex 1 triangle PDF 9.4MB |
 3 Tile set PDF 6.0MB |
 1 Hex tile PDF 6.2MB |
 3 Tile set mirrors PDF 7.4MB |
 1 Hex tile mirrors PDF 7.6MB |
 7 & 3 Tile sets PDF 4.4MB |
Over the years I kept coming back to the problem of the Eve tiling and in August 2005 finally began to make some progress. In the period 16 August 2005 to 11 December 2005 approximately 15 recursive patterns were explored, based on triangles, hexagons and six-pointed stars. From these a chronological sequence of some half dozen have been selected to illustrate the metamorphosis of the Eve tiling into the Llama tiling (made by an aperiodic, single, regular hexagon with a side rule and a vertex rule).
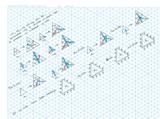
The first step equipped the 4 (first inflation) coloured triangles of the Eve tiling with letter matching rules and a 'black corner' rule, which said that the same colour must appear on each side of it. Still the periodicities persisted until a superposition layer of 'clock-sense' stripes was added, increasing the number of tile types to 8, or 13 if distinct mirror-images are counted separately. See 8 Triangle set 1 and 8 Triangle set 2. This scheme can also be thought of as a tiling by 2 hexagons and 4 triangles. 8 Triangle set 3 shows the superposition layer with some evidence of preliminary thoughts of further joining up the stripes (lines of little o's) to try to reduce the number of tile types and facilitate tile matching.
Chiral pattern shows a simpler recursive pattern of clock-sense stripes that would work as well as the previous superposition layer. In this drawing can be picked out an inflation pattern of 4 triangles and also one of 2 hexagons and 2 triangles (plus mirror-images, as always). Based on this pattern, I played with making stripes continuous across vertices and sides and with matching red to red or red to blue, and stumbled on the following scheme.
2Hex 1 triangle shows triangles (composed of 16 graph-paper triangles) of 3 kinds - those with 3 black vertices, 1 black vertex and no black vertices. The stripes anti-match (i.e. single to double) at black vertices and across sides and continue unchanged across white vertices. These may be gathered into 2 hexagon types and one triangle type (3 black vertices), plus mirror-images - the stripes are still considered to have clock-sense. The two types of hexagons are indicated by heavy single and double hexagons about their centres. Periodicities are possible unless this layer is superposed on the coloured triangles with letter labels and black corner rule of 16 August.
Introducing further changes including continuing stripes unchanged across sides reduced the number of hexagon types to one - see the heavily outlined hexagon and triangle in 1 Hex 1 triangle (triangle is composed of 16 graph-paper triangles). Still the superposition on the coloured triangles is necessary. Now there can be picked out of this drawing a star, hexagon and triangle (the triangle composed of 4 graph-paper triangles at the centre of the heavily outlined triangle). These are reproduced in 3Tile set.
The star, hexagon and triangle appearing here, 3 Tile set, have the addition of side markings, X and O. This set sheds its dependence on the coloured triangles of 16 August. The 3 tile set can be styled with shape-alone matching.
1 Hex tile. Altering the star tile, from the 3 tile set, into a hexagon and translating the function of the triangle into a vertex rule (not 3 same stripes to meet) and the function of the hexagon into a side rule (stripes to alternate at each end of a side of the new hexagonal tile) made a single hexagon tiling. The new hexagonal tile inherited the X and O side matching, which was previously transmitted through the hexagon of the 3 tile set.
3 Tile set mirrors shows the 3 tile set coloured to distinguish mirror-image tiles. (This drawing has faded in the sun.)
1 Hex tile mirrors shows the single tile version, also coloured to distinguish mirror-image tiles. The first llama-shaped (13 tile) islands of one mirror type appear.
Next, 7 & 3 Tile sets, a tracing was made of the first inflation size hexagons (sides are the diameters of the small hexagonal tiles) and 7 different types were found with their mirror-images and labelled A to G. These were found to inflate - the first inflation letter-label is in one set of parentheses, the second inflation label in 2 sets of parentheses. It was also noticed that the pattern of black and white hexagons could be described by 3 clusters of hexagons - a single hexagon, a group of 3 hexagons (later called a glugon) and a group of 7 hexagons (the inflated C-cluster). These 3 clusters replicate the functions of the tiles in the 3 tile set of 3Tile set. It was a surprise to see the 3 tile set reassert itself in the single tile tiling!
These 3 and 7 tile sets are described fully in Aperiodicity of a Functional Monotile, mentioned on the Home page, where it was found that the demonstration of possible tile arrangements was simpler if described on a 14 half-hexagons prototile set. This scheme also corresponded precisely to Grunbaum and Shephard's composition prescription and , so I thought, was the more acceptable. In a subsequent collaboration with Joshua Socolar, we found that the vertex rule was unnecessary to the aperiodicity of the single hexagon.
