Joan Taylor's Tilings
Eve Tiling and Variants
| Home |
| Eve tiling and variants |
| Rhombus seed tilings |
| Square tilings |
| Triangle and 3-fold symmetry tilings |
| Cross & 3 key tiles |
| Eve to llama tiling |
| 2 Squares tiling |
| Cube tiling |
 Penrose inspiration PDF 5.8MB |
 Periodicities PDF 5.6MB |
 Eve variants PDF 6.0MB |
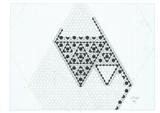 Eve rhombus PDF 5.4MB |
 Eve sub tiles PDF 6.8MB |
 Eve reverse PDF 6.6MB |
 Eve inverse PDF 9.5MB |
 Eve inverse sub tiles PDF 7.3MB |
 Eve inverse striped PDF 8.8MB |
 FBF tiling PDF 7.5MB |
 BFB tiling PDF 8.2MB |
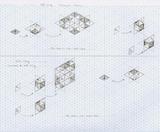 FBF and BFB sub tiles PDF 7.2MB |
 BBF tiling PDF 8.8MB |
 BBF sub tiles PDF 3.2MB |
On New Year's Eve going into 1993 I conceived a way to translate Penrose's 5-fold rhombus tiling into 3-fold symmetry and in a way that could be described by a single hexagon. This is shown in Penrose inspiration (click on the image to obtain a larger view)., where the arrow matching marks of Penrose's rhombuses are directly applied to the regular hexagonal case. Penrose's tiling can be thought of as a hierarchy of hexagons or as a heirarchy of (overlapping) regular decagons. (The Ammann-Beenker tiling as either hexagons or regular octogons.) In the 3-fold symmetric case there are only hexagons, so it seemed the limiting case.
At this time I didn't have a way to prevent the heirarchy of periodicities, see Periodicities, that the adopted matching rules permitted, but was convinced that some superposition of extra matching rules would somehow do so. Eve variants and Eve rhombus show three alternate faces of the Eve tiling. Eve substitution tiles shows a substitution scheme for the rhombus version. This tiling has an alternative designation of FFB, which stands for forwards, forwards, backwards. This refers to the orientation of the arrow markings on the tiles composing the hexagon, Penrose style. This scheme persists on all scales, viewed from the centre of 3-fold symmetry. A single hexagon always fits in the centre of each inflated hexagon. Although the arrow markings are consistent with the substitution scheme they are not sufficient to prevent the periodicities.
Eve reverse is the pattern produced on rotating through pi each of the three central rhombuses, maximally inflated. Or, if you consider the plane at infinite distance wrapping around to a point, as on the surface of on infinite sphere, then this is the view from infinity.
Eve inverse and Eve inverse sub tiles. The inverse tiling is made by rotating the whole hexagon through pi. Further details are to be found on the drawings. A striped version appears in Eve inverse striped. FBF tiling, BFB tiling and FBF and BFB sub tiles show more variations on the theme of side arrows. Here the 'thin' rhombus comes with a distinct mirror image. BBF tiling and BBF sub tiles is the last in the series.
